
« La conjecture de Duffin-Schaeffer est vraie. » Dimitris Koukoulopoulos et son collègue James Maynard, de l’Université d’Oxford, posent devant la diapositive qui annonçait leur théorème à la communauté des mathématiciens à un colloque en Italie. Image: Kevin Ford
Est-il possible d’approximer, à l’aide d’une simple fraction, un nombre comme Pi avec une précision donnée? Voilà une question qui turlupinait les mathématiciens depuis 1941 et qui est aujourd’hui élucidée.
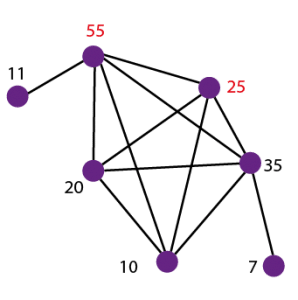
Sur ce graphe apparaissent des dénominateurs. Ils sont reliés lorsqu’ils ont au moins un facteur premier en commun, c’est-à-dire un nombre premier qui peut les diviser en donnant un entier. Par exemple, 25 et 10 peuvent tous deux être divisés par 5. Les dénominateurs non reliés, comme 11 et 20, ne partagent aucun facteur premier. C’est l’analyse du patron d’un tel graphe qui a permis aux mathématiciens de prouver que, même lorsque les dénominateurs choisis ont plusieurs facteurs premiers en commun, la conjecture de Duffin-Schaeffer tient toujours. Graphique adapté de Quanta Magazine
Ce n’est pas tous les jours qu’on prouve une conjecture mathématique, un énoncé qui se vérifie par des exemples, mais qui n’a pas été démontré hors de tout doute. C’est pourtant ce qu’a réussi Dimitris Koukoulopoulos, mathématicien à l’Université de Montréal, en validant la conjecture de Duffin-Schaeffer formulée il y a 80 ans… Une prouesse saluée par des mathématiciens du monde entier !
Cette conjecture tourne autour d’une question : est-il possible d’approximer, à l’aide d’une simple fraction, un nombre comme Pi avec une précision donnée ? Pi fait partie de la famille des nombres irrationnels.







