En quête d’une formule pour les nombres premiers
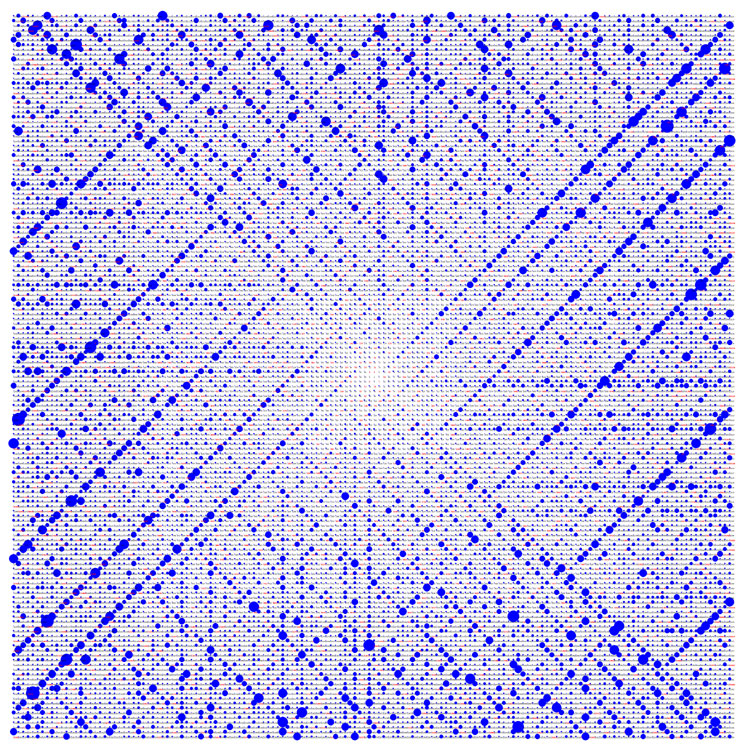
La spirale d’Ulam représente les nombres premiers et révèle un motif en spirale. Générée avec la librairie GD de PHP, par Cortexd
Y a-t-il une formule qui donne tous les nombres premiers? Ou du moins uniquement des nombres premiers? La réponse courte est ni oui ni non.
C’est une question vieille de plus de deux millénaires : comment savoir quel nombre premier suit un nombre premier pris au hasard? Par exemple, si l’on regarde la série de ces nombres divisibles uniquement par 1 et par eux-mêmes, on obtient ceci (la liste n’est pas exhaustive bien sûr) : 2, 3, 5, 7, 11, 13, 17, 19… 193, 197, 199… 827… 2 347. Quel est le prochain?
«Tous les grands mathématiciens se sont penchés sur le problème : on peut calculer combien il y a de nombres premiers avant 1 000 ou avant 10 000, mais personne n’a de formule pour trouver directement le n ième nombre premier», résume Simon Plouffe, mathématicien d’origine québécoise et professeur au Département d’informatique de l’Institut universitaire de technologie de Nantes.
En fait, pour constituer la liste des nombres premiers, on utilise une technique mise au point il y a plus de 2 000 ans par le savant grec Ératosthène. Elle consiste, à partir de la liste des nombres entiers, à rayer successivement tous les multiples de 2, puis les multiples de 3 (à part 2 et 3 eux-mêmes), et ainsi de suite jusqu’à ce qu’il ne reste que les nombres premiers, indivisibles.








