
Image: Gerd Altmann/Pixabay
Solutions
Par Jean-François Gagnon
Problème 1 : Une foule de triangles
Avec 5 points, on peut les dessiner tous pour constater qu’il est possible d’en concevoir 10 différents.
Avec 8 points, c’est plus difficile. Il faut d’abord remarquer qu’on a 8 choix pour le premier sommet, 7 pour le deuxième et 6 pour le dernier.
Mais ce n’est pas tout. Il y a plusieurs façons de choisir les mêmes points pour le même triangle : parmi les 3 points choisis, il y a 3 choix pour le premier, 2 choix pour le deuxième et 1 pour le dernier. De là on comprend que chaque triangle est compté 6 fois (3x2x1). Ainsi il y a (8×7×6)/6 = 8×7 = 56 triangles.
Avec 100 points, on a 100 x 99 x 98/6 choix = 161 700 triangles différents qu’on peut construire.
Problème 2 : Carrelage alambiqué
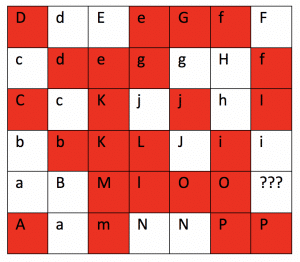
Partons du coin en bas à gauche. Nous avons identifié la seule pièce qu’il est possible de placer pour remplir cette case. Nous l’avons appelée « a », car elle commence la série et la majuscule est attribuée à la case qui a forcé ce choix. Les pièces suivantes respectent l’ordre de l’alphabet. À la fin de l’exercice, il est impossible de combler le dernier espace.
Problème 3 : Petit ou gros rabais?
Question A .







